Часть 13. We are the champions, my friends!

Приветствуем вас, наши думающие и вычисляющие друзья, в особенности наши лидеры. Вы – настоящие чемпионы духа! Мы подводим итог в данной статье первого тура «Беловской Высоты». Проведем разборы всех восьми олимпиадных задач, сведем окончательную турнирную таблицу. Укажем награждаемых и поощряемых. Короче, будет много приятного! К нашей радости, стремительно в число лидеров влетело аж 5 учеников гимназии №42 города Кемерово. И не случайно, что эти ребята потеснили некоторых из наших «небожителей». Вначале – задачи, их решения.

 

Близнецы будоражат общественность нашего города!

Данная задача вызвала наибольшее количество откликов и поистине взбудоражила думающую школьную, учительскую и любительскую общественность нашего города и иногородних участников! Семьи многих участников были также поглощены ею и многие в итоге сдались, когда до правильного решения оставалось полшага. Но подавляющее большинство участников Высоты присылало несколько вопросов встретившемуся близнецу, так, конечно, легче! Автор был свидетелем, когда для натурных экспериментов в одном из классов школы Белово была привлечена реальная пара близнецов (по счастью дело ограничилось лишь теоретическим моделированием ситуации!). Видимо для людей сказалась привлекательность и «жизненность» формулировки данной логической задачи. Ну и кому в душе не хочется обвести лжеца и рыцаря, считая последнего простаком, а первого  мошенником?!

Не случайно, что особенно сильно хотели решить данную задачу записные гуманитарии (учитель русского языка одной из беловских школ, это только где я был свидетелем). И надо сказать - не без оснований! Хотя вопрос предполагался единственным встретившемуся близнецу, но устроен он мог быть и сложно. Вот где пригодилось бы уверенное владение деепричастными оборотами, умение соединять два вопроса в один, или вовсе придумать вопрос-монстр! Тандем технаря и гуманитария мог бы принести победу, но наши победители владеют не только мыслью,  но и словом. Это приятно, особенно потому, что принято считать лишь естественные науки главными «потребителями» и «вдохновителями» математики, забывая подчас, что многие математические науки выросли из чисто гуманитарных соображений и возвращаются в виде результатов, например, в виде автоматизированного перевода, поисковых систем, экспертных систем, искусственных языков и систем распознавания текста и искусственного интеллекта.

Короче, вопрос мог быть и громоздким, но я был бы вынужден проверить и его на верность. Надо сказать, меня дико обрадовало то, что люди, правильно решившие эту задачу, придумывали второй, третий способы, как например, Каргин Александр и Смирнова Кристина. Решение Кристины и приведем сейчас.

Из двух братьев­-близнецов один – патологический лжец (всегда говорит неправду), другой всегда говорит правду. Сосед данных братьев узнал, что за то время, что он их не видел, оба брата стали отцами (у каждого появился ребенок). Во дворе дома сосед увидел одного из братьев. Какой вопрос должен задать сосед, чтобы после ответа близнеца на него, можно было безошибочно определить пол ребенка этого близнеца. Заметим, что сосед не различает близнецов по внешности, близнецы же знают все про семьи друг друга и своих детей.

Решение. Следуем за Кристиной Смирновой. Вопрос: «Мог ли твой брат ответить, что у тебя сын?»

Как отвечает честный:
если у него сын, то он ответит «нет», так как знает про своего брата что он лжец, если у него дочь, то ответит «да», по этой же причине.
Лжец ответит:
если у него сын, то ответит «нет», так как знает, что брат скажет правду, но сам он должен нам соврать, так как он - лжец. Так что однозначно «декодируем» пол ребенка вопрошаемого. Ну, и «нет» в случае дочери.

Ну а решение Демина обосновывается очень красиво и стройно в стиле новосибирской школы логики и приходит примерно к тому же вопросу. Итак, видите, как неудобно быть столь прямолинейным по жизни честный вы до мозга костей, или «лжец конченный»?! Любой знаток математики раскроет вашу тайну. Эх, в разведку бы наших победителей и призеров, таких бы делов наворотили…

Расшифровка примера из гробницы Тутанхамона

Расшифруйте пример на сложение:
КОПР + КОПР=ОРПАП
Каждая буква – это цифра, причем различные буквы обозначают различные цифры, одна и та же буква обозначает одну и ту же цифру. Старшие разряды отличны от 0 (К≠0, 0≠0). Восстановить данный пример на сложение. Ход решения приводить с обоснованием. Если задача допускает несколько решений, то привести все.

Решение. Каргина Александра. Буква О в данном примере однозначно равна 1, т.к. сумма двух К не может превышать числа 18, из этого следует, что О=1. Если О равно 1, значит П равно 2 или 3. 3 она быть равна не может, т.к. при сложении 2-х одинаковых цифр (Р+Р), нечётное число получиться не может. Значит П=2.

Если П=2, а в примере различные буквы содержат различные цифры, значит Р=6 (т.к. 6+6 в сумме получают 12). Если Р=6, а П=2, значит А=5, т.к. П+П=4, и плюс от суммирования двух Р. Если в сумме K+K=P, Р=6, а О=1, значит К=8 (т.е. 8+8=16).

Исходный вид примера таков: 8126+8126=16252 что полностью соответствует схеме.

Расшифровывать математикам приходится многое что, причем не без риска для собственной безопасности. А что, военное дело в 21 веке неотделимо от шифрования своих данных и взлома вражеских данных. Но начинать надо с легкого. Я думаю, этот  пример вполне мог быть в гробнице Тутанхамона, если бы, конечно, древние египтяне могли знать десятичную запись.

Компьютер из ничего. Только наблюдения за «столбиком».

Решим важную задачу на остатки, посильную многим нашим участникам.

Задача 6. Определить: на какую цифру заканчивается число, равное значению степени:
а) 11²⁰, б) 2²⁵, в) 3¹¹, г)13¹³¹³

Приведем решение нашего победителя Епифанцева Степана, опуская подробности. Последняя цифра произведения определяется последними цифрами сомножителей (простое умножение «столбиком»). а) Очевидно, один, умноженный на один, всегда будет один. Следовательно, 11²⁰ оканчивается на один.

Ответ: 1;
 б) 2*2=4, 4*2=8, 8*2=16, 6*2=12, 2*2=4
Через каждые четыре умножения на двойку (начиная с двойки), результат повторяется периодически, в первой степени 2, во второй 4, в третьей 8, в четвертой 6 (на конце), в пятой двойка (на конце) и т.д. Так как 25=4*6+1, то результат на конце будет двойка.

Ответ: 2
в) 3*3=9, 9*3=7 (на конце), 7*3=1 (на конце), 1*3=3, 3*3=9 и т.д. Опять периодически результат повторяется через каждые четыре умножения на тройку, начиная с тройки.
То есть, последовательность последних цифр: 3,9,7,1,3 и т.д. Так как 11=2*4+3, то

Ответ: 7
г) так как последняя цифра основания  определяет последнюю цифру результата, то можно свести к 3¹³¹³  . Так как  4*328+1=1313, то последняя цифра 3. Ответ: 3 Заметим, что можно использовать было признак делимости на 4 (период). Число составлено из последних двух цифр 13 делится  на 4 с остатком 1. То есть можно было бы найти последнюю цифру числа 20193^15678925 с таким же результатом на конце.

Разоблачен диверсант или салага снимается с довольствия

Задача 5. Иванов, Петров и Сидоров работают вместе на одном участке шахты. Кадровый работник готовит списки кандидатов на сокращение. Экспериментально доказано, что работая только вдвоем, Иванов и Петров выполняют план (дневной) за 2 часа, Иванов и Сидоров этот же объем работы выполняют за 3 часа, а Петров и Сидоров – за 10 часов. Найти время, за которое Иванов, Петров и Сидоров выполняют данный объем работы, работая вместе втроем. Кого первым нужно включить в список на сокращение (увольнение)? (Указание: отрицательная производительность труда означает, что работник – помеха). Результаты приводить точные (без округления). (7 баллов)

Приведем решение, принадлежащее  Каргину Александру, одному из наших победителей: Обозначим производительность рабочих за х,у,z – выполненная доля дневного плана в час Ивановым, Петровым и Сидоровым соответственно. Все справившиеся участники с задачей составили систему из трех уравнений: х+у=1/2; х+z=1/3; y+z=1/10. Затем сложили три уравнения, получаем производительность всей тройки рабочих: х+у+z=1/2+1/3+1/10; х+у+z= 7/15. Откуда и получаем, что трое работников выполнят всю работу за 15/7 часа. Далее, Александр Каргин остроумно не стал вычислять производительность каждого работника (этого и не требовалось) а логически обосновал целесообразность увольнения Сидорова тем, что увидел, что совместная производительность тройки рабочих меньше чем совместная производительность Иванова и Петрова. Стало быть, ату Сидорова! Надо сказать, что половина наших лидеров решила задачу правильно. В целом эту задачу можно признать стандартной по олимпиадным меркам, но, как водится,  на олимпиаде «душа просит праздника»  и хочется решить задачу изящнее и проще (без систем уравнений), на уровне смышленого второклассника или третьеклассника (не боящегося дробного ответа), «порхающего как бабочка и жалящего как пчела». Итак, подключаем воображение гидротехника и

Превращаем работников в трубы и клонируем систему труб.

Пусть наши работники представляют из себя трубы, которые к бассейну подключены (параллельно, естественно друг другу). Дневная работа состоит в наполнении бассейна водой. Труба И, П, С – наши работники. То есть, трубы И, П включенные вместе наполнят бассейн за 2 часа, трубы И, С заполнят его за 3 часа, а П и С за 10 часов. Лишние и вредные для нас трубы – это те, которые в действительности устроены так, что или не заполняют бассейн (труба-пустышка) или могут даже выкачивать из него (как насосы) воду.  Задача состоит в том, чтобы определить, за какое время три трубы, работая вместе, заполнят бассейн и если есть трубы-насосы (или пустышки), то определить их и отключить таковые из системы. А что, неплохая задачка для отрасли  ЖКХ! Заметим, что сложные технические диагностические процедуры заменяются здесь решением математической задачи. Решай  и становись героем местного жека! Кстати, вопрос, может ли быть больше одного насоса (или трубы-пустышки) среди данных трех труб? На это каждый сантехник ответит, что нет – иначе какая-нибудь пара труб никогда не заполнила бассейн вопреки условию задачи. Там все-таки каждая пара труб справляется с задачей наполнения бассейна, пусть и с разными временными показателями. Стало быть, если труба-насос (или пустышка) и есть, то только одна. Вывод получен без всяких вычислений, а только после небольшого наблюдения над условием. Как говорил, Козьма Прутков, «бросая камешки в воду, наблюдай круги, ими образуемые, иначе это занятие будет простою забавою».
  Теперь мысленно клонируем данную систему, то есть, подключим точно такие же три трубы идентичные трубам И, П, С соответственно. Теперь у нас 6 труб, а именно: И, П, С, И, П, С. Включим все шесть труб одновременно и позволим работать системе 30 часов (заметим что 30 делится и на 2 и на 3 и на 10).  В этих шести трубах есть пара И, П она заполнит 15 бассейнов, одновременно пара И, С заполнит 30:3=10 бассейнов, и пара П, С заполнит 30:10=3 бассейна. Всего данная система заполнит 15+10+3=28 бассейнов за 30 часов. То есть данная система заполнит 1 бассейн за 30/28=15/14 часов. Но понятно, что она сработает в два раза быстрее, чем исходная система И, П, С. Следовательно, система из трех труб заполнит бассейн за (15*2)/14=15/7 часов. Теперь так же вслед за Сашей Каргиным визуально оценим 15/7>2, следовательно, труба С – насос, выкачивающая из бассейна драгоценную воду и подлежит отключению от бассейна.  А если бы равны оказались – тогда все равно бы отключил С. Понятно, что это решение более изящно и экономно, практически исключает возможность ошибиться в расчетах. Эта задача и подобные им запросто могут встретиться на ЕГЭ в профильной математике (и встречались вашему покорному слуге!) Иметь надо много сценариев решения задачи, чтобы один из них безошибочно сработал как автомат Калашникова и не утомил бы ваш мозг на экзамене.

Вагоны – это не только уголь, но и 2, 3, 6, 10, 15 и т.д. попарных сумм масс!

Задача 8. Весы, взвешивающие вагоны, испортились настолько, что не могут взвесить отдельный вагон, а только взвешивают пару вагонов, показывая их суммарный вес. Для данных четырех вагонов получены всевозможные попарные суммы масс: 185т, 200т, 215т, 220т, 235т, 250т. Найти вес каждого вагона. Если решений несколько, то привести все решения. Ответ обосновать. (7 баллов).

Данную задачу полностью решили лишь Демин Дмитрий (Аллиллуя победителю!) и Макушкина Елизавета (молодец, семиклассница!) с полным обоснованием. Ключ к ее логическому обоснованию лежал в статье №7 (как мы и писали ранее) где говорилось про различные 4 числа, надо было сравнить между собой их попарные суммы. Справедливости ради надо сказать, что сперва участники получили некорректные от составителя  данные, которые затем были исправлены. Итак, в студию – решение победителя Демина Дмитрия (с опусканием малозначащих деталей)!

Не будем сразу пытаться «ваять» системы уравнений. Логически причешем и выудим какую-нибудь полезную информацию о вагонах. Пусть наши числа а,b,c,d. Имеем шесть попарных сумм: а+b, a+c, b+c, b+d, a+d, c+d. По условию они равны 185т, 200т, 215т, 220т, 235т, 250т. Видно, что они все различны. Что это нам дает? Это значит, не много – не мало, что наши четыре вагона тоже различны по весам! В самом деле, в противном случае, пусть например, а=b. Тогда, a+c=b+c, a+d=b+d. Но ведь нет таких двух пар равных сумм, все шесть сумм различны! Итак, имеем, что a<b<c<d. Из свойств числовых неравенств имеем: самое маленькое число (из шести сумм) а+b, самое большое c+d (не забываем что все суммы - различны). Затем, точно после а+b самое маленькое а+с. Затем может быть b+c, а потом самое маленькое a+d. А может быть и наоборот, a+d<b+c. . Поясним мысль. Пусть 1<2<3<8. Здесь  1+8>2+3. Теперь 1<8<9<10. Здесь 8+9>1+10 . То есть, в первом случае масса двух крайних больше, во втором- меньше суммарной массы двух средних вагонов. Но самые две большие тогда b+d и наконец с+d. Так что имеем две развилки:

Первая система шести уравнений:
a+b=185; a+c=200;b+c=215; a+d=220;b+d=235; c+d=250 ; (1)

И вторая система шести уравнений:
a+b=185; a+c=200;b+c=220; a+d=215;b+d=235; c+d=250 ; (2)

Решим системы следующим образом. a+b+c найдем из первых трех уравнений системы, сложив их, а затем разделив на 2.  Из (1)

a+b+c=300. Откуда, с =115, b=100,a=85, ну а d найдем из четвертого уравнения:

d=220-a=220-85=135. Первое решение: 85т;100т;115т;135т

Из системы (2) имеем: a+b+c=302,5.

Откуда c=117,5, b=102,5,a=82,5,d=215-a=215-82,5=132,5т

Ответ: 1) 85т;100т;115т;135т; 2) 82,5т; 102,5т,117,5т,132,5т

Заметим, что сейчас и способ получения именно этих двух решений обоснован. А так, вообще-то удивительно, что вроде бы подробные данные не определяют однозначно массы вагонов. Возможны две ситуации, оказывается! Реальность интереснее и многообразней, чем кажется на первый взгляд. Хотя использовали мы общеизвестные вещи, на мой взгляд. Но, как говорил Конфуций: «тот, кто, обращаясь к старому, способен открывать новое, достоин быть учителем!». Кстати, когда китайцы говорят «Учитель», считайте, что они говорят о некоем божественном существе. Подобная задача предполагала медленное, но верное вживание в нее и фиксацию постепенных продвижений и обоснований перед связным и полным оформлением «семибального» решения как никакая другая и неудивительно, что оказалась практически неподвластна (имея в виду полное решение) нашим лидерам, не считая Лизы и Дмитрия. Приведем сразу задачу №7 которую было просто решить.

Весы, взвешивающие вагоны, испортились настолько, что не могут взвесить отдельный вагон, а только взвешивают пару вагонов, показывая суммарный вес. Для 3-х данных вагонов получены их попарные суммы: 185т, 190т, 200т. Найти вес каждого вагона из данной тройки. (7 баллов)

Решение. Тут все просто. Составляем систему из трех уравнений.

x+y=185; x+z=190; y+z=200. Теперь складываем три уравнения и получаем следствие: 2(x+y+z)=575

делим обе полученные части на 2:

x+y+z=287,5

Вычитаем из следствия третье уравнение и находим х
х=87,5. Поступая аналогично со вторым и первым уравнениями находим y,z соответственно. y=97,5; z=102,5

Ответ: 87,5 тонн, 97,5 тонн, 102,5 тонн

Кубок титанов обрел своего победителя -  математика Ярымбаша!

Приведем логическую задачу №4 про спортсменов

В Суперфинал Кубка Героев пауэрлифтинга вышли Евгений Ярымбаш, Михаил Кокляев и Андрей Маланичев. Перед выступлением они дали интервью Сергею Бадюку, где взвесили свои шансы.

Маланичев заявил: «Кокляев – не самый сильный». Ярымбаш сказал «Кокляев посильнее меня будет». Кокляев же заявил: «Я сильнее Андрея». После того, как все сделали свои подходы, оказалось, что победитель ошибся в прогнозе, а другие сказали правду.

Вопросы:
1) Смог ли победить Михаил Кокляев?

2) Кто победил в Суперфинале?

Пользоваться лишь условиями задачи.

Решение. Следуем за Данилом Чехом. Допустим, Кокляев победил. Но он тогда должен был ошибиться. Однако его утверждение: «Я сильнее Андрея» не похоже на ошибку, ведь победитель и вправду сильнее остальных двух. Следовательно, Кокляев не победил.

Маланичев также не является в этот год победителем, ведь он сказал истину: «Кокляев не самый сильный». Мы ведь уже выяснили, что это так. Но скромный Ярымбаш вполне мог бы оказаться победителем, если задача не противоречива, он в этом случае ошибся бы (причем единственным). Проверяем: 1. Ярымбаш,  2. Кокляев, 3. Маланичев. Все связно при такой турнирной таблице и укладывается в условие задачи. В самом деле, Кокляев поставил себя выше Маланичева, а Маланичев правильно оценил шансы Кокляева. Надо привести было эту таблицу, ведь могло оказаться и так что решения нет, т.е задача составлена не корректно. Ответ: Нет, Ярымбаш.

    Надо сказать, что данные спортсмены из постсоветского пространства – герои пауэрлифтеров нашего города, и вообще, они - настоящие герои спорта! Надеемся, что мы не задели чувств их фанатов и болельщиков. Кстати, Евгений Ярымбаш, неоднократный победитель престижнейшего Кубка Титанов, говорил в интервью, что у него отлично шла математика и физика в школе, и он вполне мог бы поступить на математический факультет. Здоровое тело – продукт здорового духа, многие действующие математики – отличные спортсмены в разных видах спорта. Побеждали они, прежде всего, себя! Может, мы и расскажем о них в дальнейшем. Вот и наш  перспективный Данил Чех – увлеченный баскетболист, не пропускающий ни одной тренировки и игры.

Рисуй и выигрывай

Ну и наконец, геометрическая задача №3. Даны 4 прямые, каждая из которых пересекает не меньше одной другой прямой. Сколько всего точек пересечения может быть. Рассмотреть все возможные конфигурации.

Решение. Вообще-то предполагались  пространственные конфигурации, но, так и быть, юные и не совсем юные по школьным меркам ребята  решили все делать на плоскости.

Все прислали рисунки, некоторые без теста решения, а только лишь рисунок и количество точек пересечения. Итак, одна точка может быть, когда у нас пучок прямых, через нее проходящий. Две точки быть не может на плоскости. Три точки могут быть вот как: обычный треугольник, образованный тремя прямыми, а потом четвертая прямая  проходит через какую-нибудь точку пересечения, параллельно одной из прямых. Ну четыре точки  просто, любой например, параллелограмм. Пять точек  так получаем, например, рисуем произвольный треугольник АВС, затем треугольник АDE, где АD, AE – продолжения сторон АB, AC за точку А, BC параллельна DE. Ну и 6 точек, когда каждая пара из 4 прямых пересекается и все эти точки различны. Как раз и получается число сочетаний из 4 элементов  по 2. Задача несложная типично наглядная, но таких задачек бы и побольше -  глядишь, народ не боялся бы геометрии как черт ладана…

Наши участники поощряются!

Нельзя не отметить преподавателя математики «кемеровского десанта» Наталью Гурьянову. Не случайно, что у нее и победитель и призер Высоты и еще много достойных результатов семиклассников (!) и шестиклассницы Филатовой Лизы. Наталья Гурьянова регулярно решает с учениками олимпиадные задачи и активно сама участвует в тренировочном процессе с олимпиадниками Всеросса.  Например, участвовала в работе физико-математической смены в «Сибирской сказке» в октябре и т.д. Без излишнего пафоса такие зажигающие любовью к своему делу и квалифицированные преподаватели – залог будущего Кузбасса!  Нельзя не отметить также преподавателей математики школы№32 и гимназии №1 Татьяну Бузынину и Евгению Челяеву. Их представители:  победитель, лидер и два призера нашей Высоты.

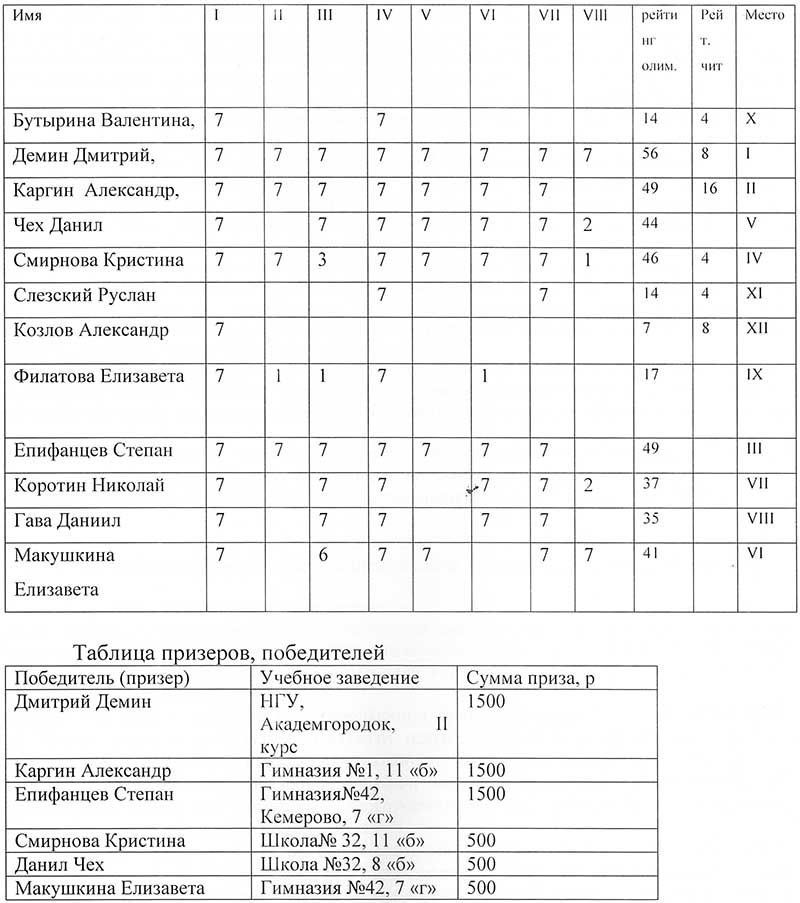
Итак, окончательная турнирная таблица:

Наши люди поднимаются и вне «Высоты»!

Пока писались эти строки, пришла информация, что наш призер Кристина Смирнова прошла муниципальный этап и отобралась в региональный этап Всеросса по математике. Сердечно поздравляем Кристину и ее родителей с успехом! Заметим, что  в прошлом году было призовое место на этом же муниципальном туре  и налицо качественный прогресс. Впереди другие высоты. Целых два тура на регионе. Необходимо серьезно отнестись к тренировке, решению задач прошлых лет из олимпиадных сборников, в том числе и международного этапа, например, подтянуть геометрию, комбинаторику и целые числа (всего-навсего то!). Епифанцев Степан, наш победитель, выиграл выездные математические турниры в Томске. Он, напомним, еще семиклассник и «сражался» на равных со второкурсником Дмитрием Деминым. Надеемся, что задачи «Высоты» причастны к успехам наших бриллиантов и откроют новые имена в дальнейшем на следующих турах (почему бы не помечтать об этом?). Ну, а Данил Чех занял  уверенное третье место на Всероссе в муниципальном туре, набрав баллов  57. Что ж, ставить дерзкие, амбициозные задачи, активно участвовать в математической турнирной хронике Белова, Сибири, России, тренируясь, возвращаться к «проигрышным» заданиям – вот, что надо уяснить Данилу и его родителям и тогда успехи не заставят себя долго ждать, а окружающие скажут «везет же умному»! Уверены, что, например, Данила очень хорошо прокачали наши задачки в качественном смысле. Семиклассница Макушкина Елизавета ничем не уступает победителям  и единственная из школьников, решившая последнюю задачу. Не говоря уже о шестикласснице Лизе Филатовой, оттеснившей солдата, программиста и абитуриентку. Мы ждали и знали, что «Высота» всколыхнет таланты Белово и Кузбасса. Талант, если он есть, никогда не сможешь зарыть в землю!

Родитель, воспитай своего Магнуса Карлсена!

Мы твердо убеждены в том, что в успехе чада  львиная доля заслуги принадлежит родителям, как уже говорилось. Положительные метаморфозы в познании мира – процедура, которую надо готовить кропотливо и желать. Давайте обратимся к наглядному примеру, который очень современен и поучителен.

Недавно завершился матч за шахматную корону между Чемпионом мира (трехкратным теперь) из Норвегии Магнусом Карлсеном и представляющим Россию Сергеем Карякиным. До матча все прогнозы экспертов были на стороне Магнуса. Все были единодушны, что до сих пор никто так не доминировал в шахматном мире как Моцарт от шахмат (как его окрестили западные журналисты). Каждый ход награждается эпитетом «гениальный». Он превысил рекордный рейтинг Каспарова несколько лет назад и разгромил в двух матчах индийца Ананда. Дошло даже до того, что Президент ФИДЕ (всемирной шахматной организации) Кирсан Илюмжинов (на фото с Магнусом) сказал, что болеть он будет за россиянина, так не «интересно болеть за компьютер»! Напомним, что сильнейшие компьютерные программы давно играют сильнее человека. Учтем, что, мягко говоря, Норвегия, где родился и вырос Магнус – страна совсем не шахматная в отличие от Украины (где родился Карякин) и России, где ему были предложены отличные условия работы и тренерский штаб.

И достаточно поздно по нынешним временам (в 8 лет) стал играть в шахматы, плотно занимаясь ими. Но главная заслуга к приобщению к аналитическому мышлению и к способности к концентрации принадлежит его отцу - Хенрику Карлсену, нефтянику – инженеру и самому в прошлом любителю-шахматисту. Ему пришлось оставить работу чтобы сопровождать сына на разные турниры, бывали моменты, что семье пришлось сдавать в аренду дом и распродавать вещи, машину, чтоб покрыть недостаток в средствах для поездок ли на турниры или для того чтобы нанять репетиторов и тренеров. Конечно, была безграничная вера в талант сына, которого «никогда не считали вундеркиндом». Пока Магнус не стал гроссмейстером, помощь и финансирование со стороны частных и государственных программ оставляли желать лучшего.

Сейчас же у норвежского Капабланки миллионные спонсорские контракты, он является лицом многих брендов от одежды до IT продуктов.

После завоевания короны в третий раз Магнус, поблагодаривший друзей и семью,  сказал «Отец, ты много значишь для меня».

«Вечернее Белово» не отстает «La Repubblica»!

Для беловских и кузбасских газет скорее в диковинку в наше время такие олимпиады и конкурсы. Хотя в мировой истории популяризации математики и в советский период, на территории СССР и в странах «восточного блока» частенько бывали случаи размещения вкусных, проблемных, а то и «не решаемых» задач на страницах газет. Например, многие кузбасские олимпиадники из тех, кто был в «Сибирской сказке», знают один из таких случаев, когда американский логик  Джон Буллос на страницах итальянской газеты «La Repubblica» в 1992 году разместил так называемую «самую сложную логическую головоломку». В качестве автора задачи указывался Раймонд Смаллиан.

Она очень увлекательная. Приведем ее. Есть три бога: A, B и C, которые являются богами истины, лжи и случая в произвольном порядке. Бог истины всегда говорит правду, бог лжи — всегда обманывает, бог случая может говорить и правду, и ложь в произвольном порядке. Требуется определить богов, задав 3 вопроса, на которые можно ответить «да» или «нет». Каждый вопрос задаётся только одному богу. Боги понимают язык, но отвечают на своём языке, в котором есть 2 слова «da» и «ja», причём неизвестно, какое слово обозначает «да», а какое «нет».

Как-то раз Конфуций спросил своего ученика: «Ты считаешь меня многоученым?». «А разве нет?» — ответил тот. «Нет, — сказал Конфуций, я лишь связываю все воедино». Так лаконично и по-сути о своей профессии, пожалуй,  может сказать любой математик. Хотя, математика - не только про это, а еще и нечто большее.

Интересно, сколько бы задач из Беловской Высоты решил  китайский мудрец без подготовки за 4 часа?

Продолжение следует…

Саркисян Эрнест, математик, тренер по олимпиадной математике
email Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript., тел: 89069235059